質量工具之故障樹分析FTA

FTA的數學基礎

我們前文提到，故障樹分析FTA可以用于系統設計、安全分析甚至是根本原因分析，既可以做定性分析又可以做定量分析，是全能型的分析技術。

故障樹分析的基礎工具是故障樹圖，從特定的故障事件開始， 利用故障樹考察可能引起該事件發生的各種原因事件及其相互關系。

故障樹通過事件符號和邏輯門符號表達事件、原因及其相互關系，是一種利用布爾代數(又稱布爾邏輯) 符號演繹地表示特定故障事件 發生原因及其邏輯關系的邏輯樹圖。

為了進行故障樹的定性分析和定量分析，需要建立故障樹的數學模型，寫出它的數學表達式。

布爾代數是故障樹分析的數學基礎。布爾代數是集合論的一部分，是一種邏輯運算方法 它特別適合于描述僅能取兩種對立狀態之一的事物。

故障樹中的事件只能取故障發生或不發生兩種狀態之一，不存在任何中間狀態，并且故障樹的事件之間的關系是邏輯關系，所以可以用布爾代數來表現故障樹。

 

 

集合的基本概念

· 集合：簡稱集，是現代數學中一個重要的基本概念。集合是“確定的一堆東西”，是指具有某種特定性質的具體的或抽象的對象匯總而成的集體；集合里的“東西”是構成集合的對象，這些對象則稱為集合元素。

現代的集合一般被定義為：由一個或多個確定的元素所構成的整體。從最普遍的意義上說，具體確定的可以區分的若干事務(事項、事件)的全體就是集合，其中的事務叫做元素。

通常用大寫字母如A、B、S、T、...表示集合，而用小寫字母如a、b、x、y、...表示集合的元素。

比如，魚骨圖中，六個主刺元素 {Man, Machine, Material, Method, Measurement, Enviroment} 構成原因Causes的集合，每個主刺下可以再分很多小刺形成子集。

o 空集不包含任何元素，記為∅。空集是特殊的集合。

o x是缺陷集合A的元素，則稱x屬于A，記作x∈A。

o y不是缺陷集合A的元素，則稱y不屬于A，記為y∉A。

o 集合A中元素的個數為集合中的元數，記作|A|。

o 集合中的元素不能重復出現，集合中的元素無順序之分。

· 集合的表示方法：

集合有如下幾種表示方法：

o 列舉法，列出集合的所有元素，并用花括號括起來。

例如，在質量管理軟件QMS中，某公司質量部分別收集某個系列的兩個產品在一個月內發生的缺陷類型，其缺陷集合分別是A和B，A={a，b，c，d，e，x}，B={f，b，g，d，h，y}。

 

 

o 描述法，將集合中元素的共同屬性描述出來。

例如，在質量管理軟件QMS中，設所有特殊特性的集合為T，關鍵特性、重要特性和一般特性的集合分別是C、S和G，則C={x|x∈T}。

o 圖像法，是一種利用二維平面上的點集表示集合的方法。一般用平面上的矩形或圓形表示一個集合，是集合的一種直觀的圖形表示法。

o 區間法，用數軸、無窮大、無窮小、開區間、閉區間 、半開半閉區間表示。數學分析中，最常遇到的實數集的子集是區間。

o 符號法，有些集合可以用一些特殊符號表示。例如，R：實數集合(包括有理數和無理數)；∅：空集(不含有任何元素的集合)。

 

 

· 有限集和無限集：集合中元素的數目稱為集合的基數，集合A的基數記作card(A)。當其為有限大時，集合A稱為有限集，反之則為無限集。 一般的，把含有有限個元素的集合叫做有限集，含無限個元素的集合叫做無限集。

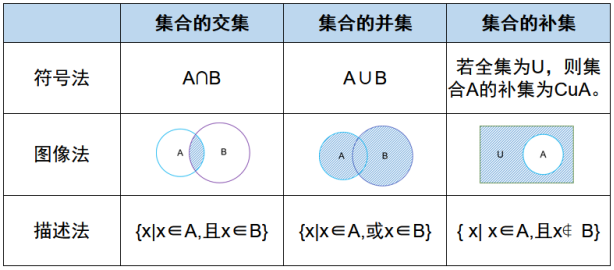
· 交集：由屬于A且屬于B的相同元素組成的集合，記作A∩B(或B∩A)，讀作“A交B”(或“B交A”)，即A∩B={x|x∈A，且x∈B}。注意交集越交越少。若A包含B，則A∩B=B，A∪B=A。

例如，上面A和B兩個缺陷集合的交集A∩B={b，d}。

· 并集：由所有屬于集合A或屬于集合B的元素所組成的集合，記作A∪B(或B∪A)，讀作“A并B”(或“B并A”)，即A∪B={x|x∈A,或x∈B}。注意并集越并越多，這與交集的情況正相反。

例如，上面A和B兩個缺陷集合的并集A∪B={a，b，c，d，e，f，g，h，x，y}。

 

 

 

· 子集：設S，T是兩個集合，如果S的所有元素都屬于T，即x∈S ⇒ x∈T，則稱S是T的子集，記為S⊆T，讀作“S含于T”。 符號⊆讀作“包含于”，表示該符號左邊的集合中的元素全部是該符號右邊集合的元素。對任何集合，都有S⊆S，∅⊆S。

o 相等集合：如果集合X是集合Y的子集，且集合Y是集合X的子集，此時，集合X與集合Y中的元素相同，因此集合X與集合Y相等。

o 空集∅是任何一個集合的子集。

· 真子集：如果M是N的一個子集，即M⊆N，但在N中存在一個元素p不屬于M ，即M?N，則稱M是N的一個真子集。

o 空集∅是任意一個非空集合Ω的真子集。

· 補集：一般指絕對補集。

假設質量管理軟件中的某個系列產品的所有缺陷的集合為F，那么A和B都是F的一個子集，由F中所有不屬于A或B的元素組成的集合，叫做子集A或B在F中的絕對補集。

在集合論和數學的其他分支中，存在補集的兩種定義：相對補集和絕對補集。

1）相對補集：針對缺陷集合A和B，由屬于A而不屬于B的元素組成的集合，稱為B關于A的相對補集，記作A-B或A\B，即A-B={ x| x∈A,且x∉B}={a，c，e，x}。

2）絕對補集：假設某公司產品缺陷的全集為U，有A⊆U，則A關于全集合U的相對補集稱為A的絕對補集(或簡稱補集)，記作A'或~A或CuA。

· 冪集：針對缺陷集合A，由集合A所有子集組成的集合，稱為集合A的冪集，記作2A={ x| x⊆A} [注：也有記作P(A)或CuA]。對于冪集有定理如下：若集合A是由n個元素所組成的有限集合，A的冪集的基數等于2的有限集A的基數次冪。

 

 

布爾代數運算法則

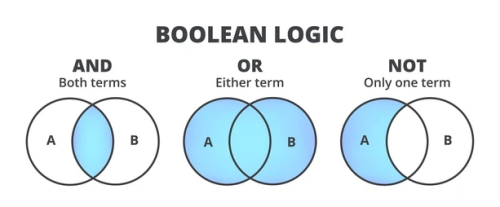
在布爾代數中， 與集合的“并” 相對應的是邏輯和運算，記作”+“；與集合的“交” 相對應的是邏輯積運算，記作”·“。

故障樹中的邏輯或門(OR)對應于布爾代數的邏輯和運算，兩個事件為并聯； 邏輯與門(AND)對應于邏輯積運算，兩個事件為串聯。

傳統的加減乘除四則運算反映的是事物間的數量關系，而布爾運算則反映的是事物間的因果關系。與普通代數四則運算一樣，布爾代數的運算也遵循基本的運算法則。

布爾代數中的變量代表一種狀態或概念，數值1或0并不是表示變量在數值上的差別，而是代表狀態與概念存在與否的符號。布爾代數主要運算法則有：結合律，交換律，分配律，吸收律，冪等律等。

下面列出了故障樹分析中常用到的布爾代數運算法則：

交換律：A·B=B·A；A+B=B+A；

結合律：A·(B·C)=(A·B)·C；A+(B+C)=(A+B)+C；

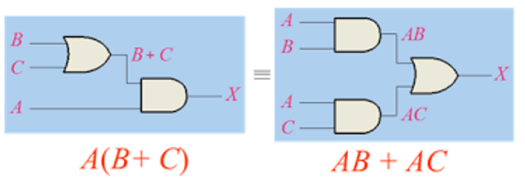
分配律：A·(B+C)=A·B+A·C；A+(B·C)=(A+B)·(A+C)；

吸收律：A·(A+B)=A；A+A·B=A；

 

 

冪等律：A·A=A；A+A=A；

互補律：A·A'=∅=0；A+A'=Ω=1；

對合律：(A')'=A；

重疊律：A+A'B=B'+BA=A+B；

摩根定律：(A+B)'=A'+B'；(A·B)'=A'+B'

 

布爾代數表達式的簡化

把故障樹中連接各事件的邏輯門用相應的布爾代數邏輯運算表現， 就得到了故障樹的布爾表達式。 一般地， 可以自上而下地把故障樹逐步展開， 得到其布爾表達式。

從上面布爾代數運算法則的介紹中，我們不難發現，等式兩邊的表達式雖然不同，但卻是等價的，邏輯功能是相同的。

也就是說，同一故障樹可以有不同的表達形式，每一表達式都可以畫出與其相應的邏輯圖。

邏輯表達式最簡單的標準有兩個：一是所含乘積項的個數最少；二是在前一條件下，每個乘積項中變量的個數也最少。

常用的化簡方法有兩種：代數法和卡諾圖法。

1. 代數法

代數法，又叫公式法，利用布爾代數的基本運算法則，對較復雜的布爾代數式進行演算化簡的方法。如何使布爾代數式達到最簡，在很大程度上依賴人們對布爾運算掌握的熟練程度和實踐經驗。下面是幾種常用的化簡方法。

1）并項法

利用互補律：A+A'=1，并項后消去變量。

例如：Y = A·B·C+A'·B·C = (A+A')B·C = B·C

2）吸收法

利用吸收律：A+A·B=A，吸收多余項，消去多余變量。

例如：Y = A·B+A·B·C = (A·B)+(A·B)C = AB，或 Y = A·B(1+C) = A·B；

 

 

3）消去法

利用吸收律、分配律、摩根定律等消去多余因子。

例如：Y = A·B+A'·C+B'·C = A·B+(A'+B')·C = A·B+(A·B)'·C = (A·B)+(A·B)'·C = A·B+C

4）配項法

利用互補律A+A'=1，A+1=1等，先把一項拆成兩項，再重新與其他項組合進行化簡，消去更多的項。

例如：Y = A·B+B·C+(A·C)' = A·B(C+C')+B·C+A·C' = A·B·C+A·B·C'+B·C+A·C' = (A+1)B·C十A·C'(B+1) = B·C+A·C'

通過代數法化簡表達式，沒有一個固定的模式，往往要綜合運用多種方法，逐步積累經驗才能運用自如。

2. 卡諾圖法

用代數法化簡布爾表達式，需要依賴經驗和技巧，有些復雜表達式，很難通過代數法求得最簡形式。

卡諾圖化簡法是一種更加系統并有統一規則可循的邏輯函數化簡法，它是邏輯函數的最小項按相鄰關系排列的方格圖，具有幾何直觀性這一明顯的特點，在變量較少(不超過六個)的情況下比較方便，且能得到最簡結果。

此法由卡諾(M.Karnaugh)于1953年提出，感興趣的讀者可以自行查閱資料了解。