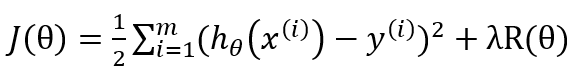
其中J（θ）， 為W^T*X和Y的函數(shù)。目標函數(shù)包含兩部分內容，正則項用于控制模型的復雜度（最小化結構風險函數(shù)），損失用于度量擬合誤差（通常使用均方誤差），目標函數(shù)通常為w的凸函數(shù)。正則項參數(shù) λ>0（regParam）為最小化誤差和模型復雜度之間提供了一種折中（如，用來避免過擬合）。

線性回歸算法的整個步驟如下：

（1）給定訓練數(shù)據(jù)樣本集

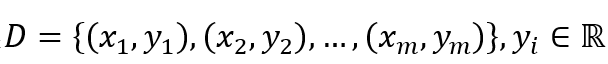
選取初值θ0，給定收斂容差 ε，最大迭代次數(shù)K，然后解下面優(yōu)化問題：

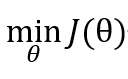
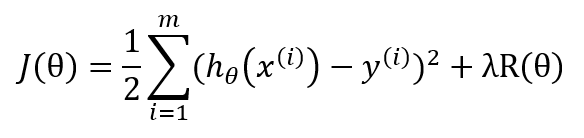
（2）采取下面公式更新θ

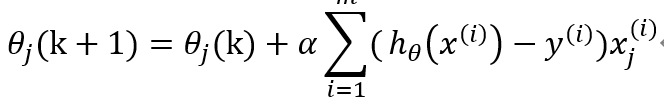
（3）當或者k<K ,輸出θ，否則轉步驟2.

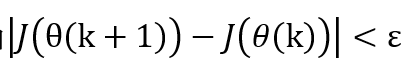
（4）構造回歸決策函數(shù)

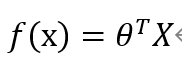
線性回歸適合分布式實現(xiàn)，能支持大數(shù)據(jù)量建模。

線性回歸算法假設每個影響因素與目標之間是線性關系，并通過特征選擇，得到關鍵影響因素的線性回歸系統(tǒng)。該算法是利用數(shù)理統(tǒng)計中回歸分析，來確定兩種或兩種以上變量間相互依賴的定量關系的一種統(tǒng)計方法，通過凸優(yōu)化的方法進行求解。在實際業(yè)務中應用十分廣泛。下面演示下Tempo機器學習平臺中線性回歸算法的使用方法。

數(shù)據(jù)格式

必須設置類屬性（輸出），且類屬性（輸出）必須是連續(xù)型（數(shù)值）；

非類屬性（輸入）可以是連續(xù)型（數(shù)值）也可以是離散型（名詞）；

參數(shù)說明

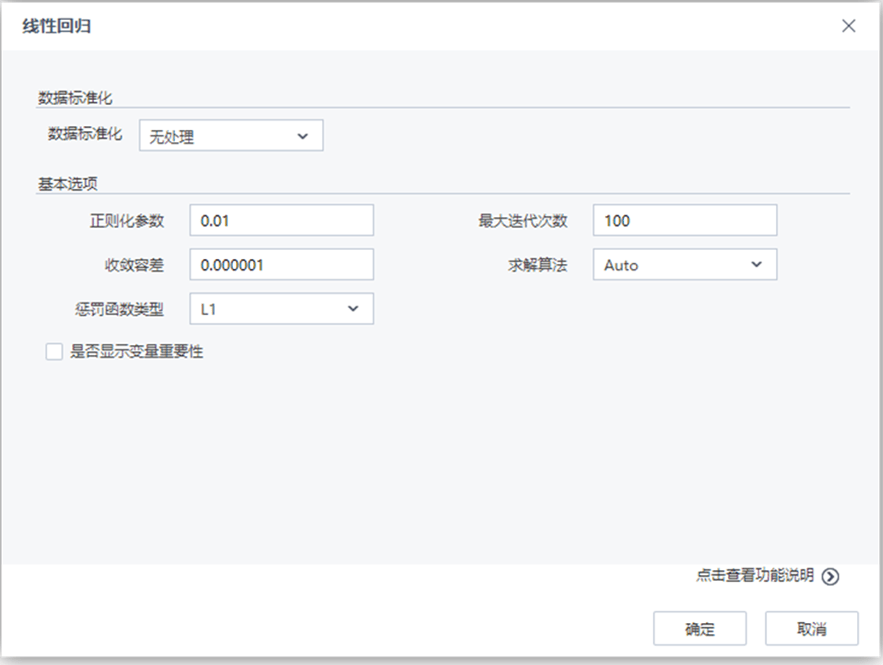
參數(shù) 類型 描述 數(shù)據(jù)標準化 下拉框 設置數(shù)據(jù)標準化的方法，字符型，取值范圍：無處理，歸一化，標準化，默認值為無處理 取值區(qū)間下限 文本框 設置歸一化取值區(qū)間下限，浮點型，取值范圍：[0,∞)，默認值為0 取值區(qū)間上限 文本框 設置歸一化取值區(qū)間上限，浮點型，取值范圍：[0,∞)，默認值為1 正則化參數(shù) 文本框 正則化參數(shù)控制機器的復雜度，浮點型，取值范圍：[0,∞)，默認值為0.01 收斂容差 文本框 設置終止迭代的誤差界，浮點型，取值范圍：[0,∞)，默認值為0.000001 最大迭代次數(shù) 文本框 設置最大迭代次數(shù)，整型，取值范圍：[1,∞)，默認值為100 罰函數(shù)類型 下拉框 設置懲罰函數(shù)類型，0對應L2罰函數(shù)，1對應L1罰函數(shù)，(0,1)之間對應L1和L2的組合罰函數(shù)。浮點型，取值范圍：[0,1]，默認值為0 求解方法 下拉框 選擇線性回歸的求解方法，文本型，取值范圍：Auto，L-BFGS,Normal （Normal->加權最小二乘法，L-BFGS->牛頓法，Auto->算法自動選取（L-BFGS,Normal）中的一種）。默認值為Auto 是否顯示變量重要性 復選框 用戶選擇是否分析每個變量對于回歸結果的影響程度，如果選擇是，則在洞察中顯示參與建模的每個變量對于模型的貢獻程度情況

結果說明

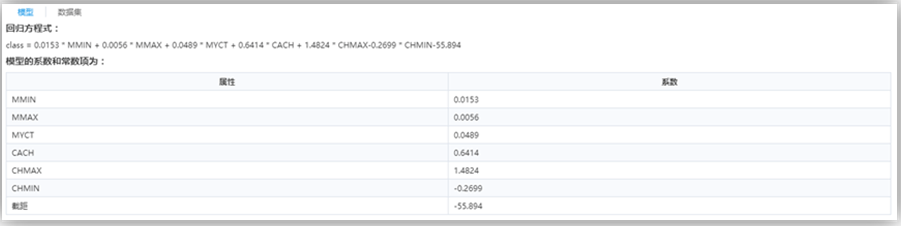
線性回歸的方程及其系數(shù)。

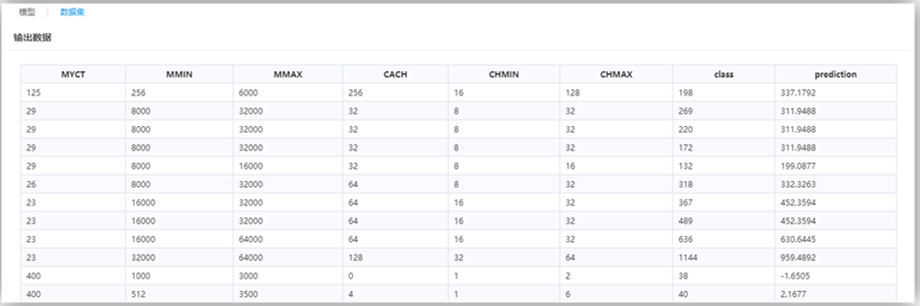
最后一列屬性“prediction”為回歸預測列。

演示示例

構建如下流程：

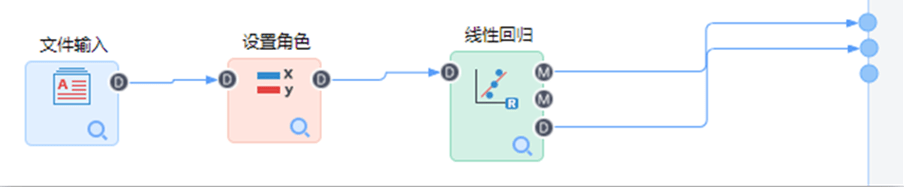
【文件輸入】節(jié)點配置如下：

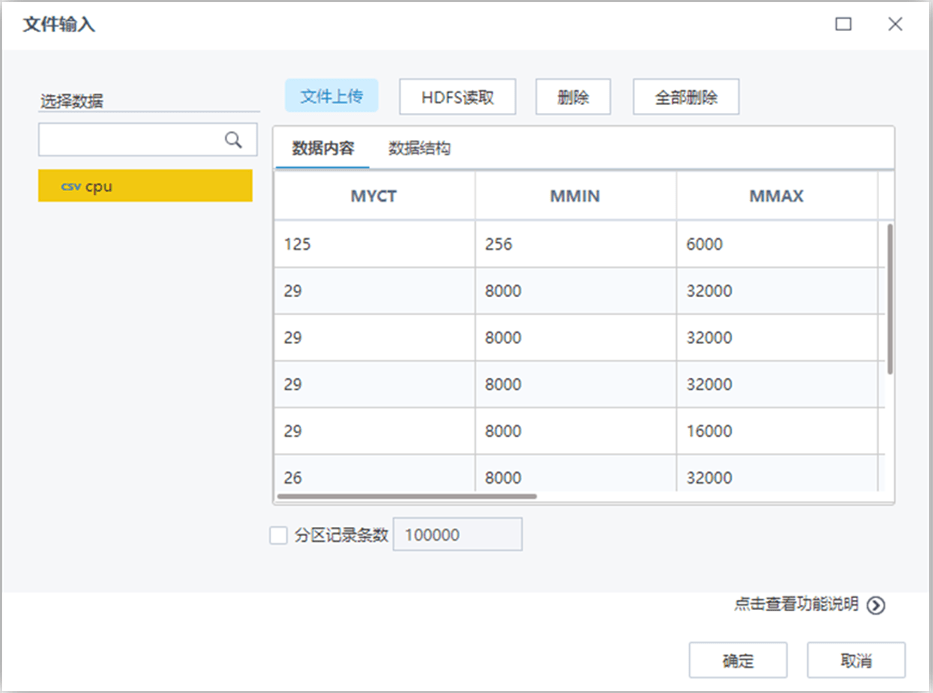
【設置角色】節(jié)點配置如下：

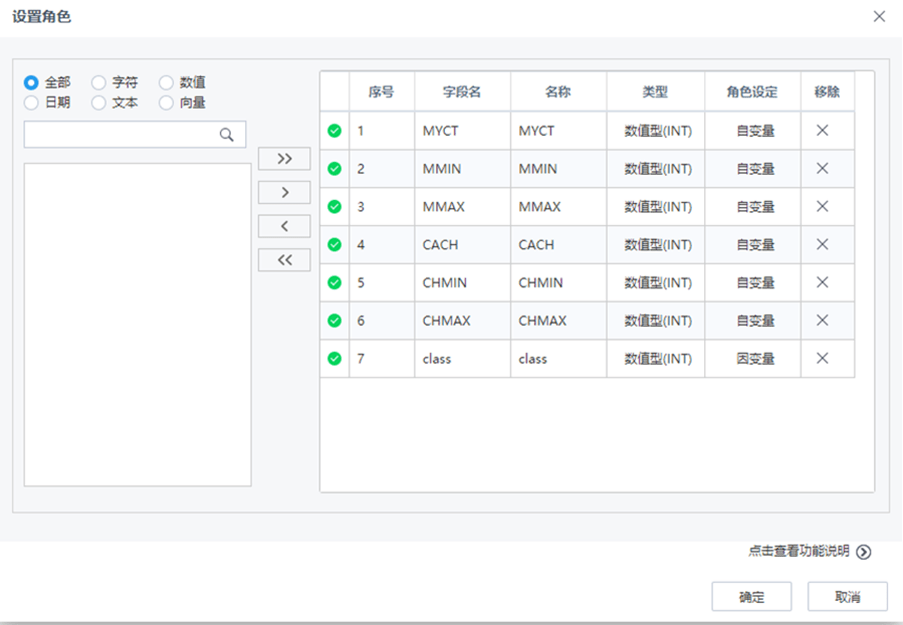
【線性回歸】節(jié)點配置如下：

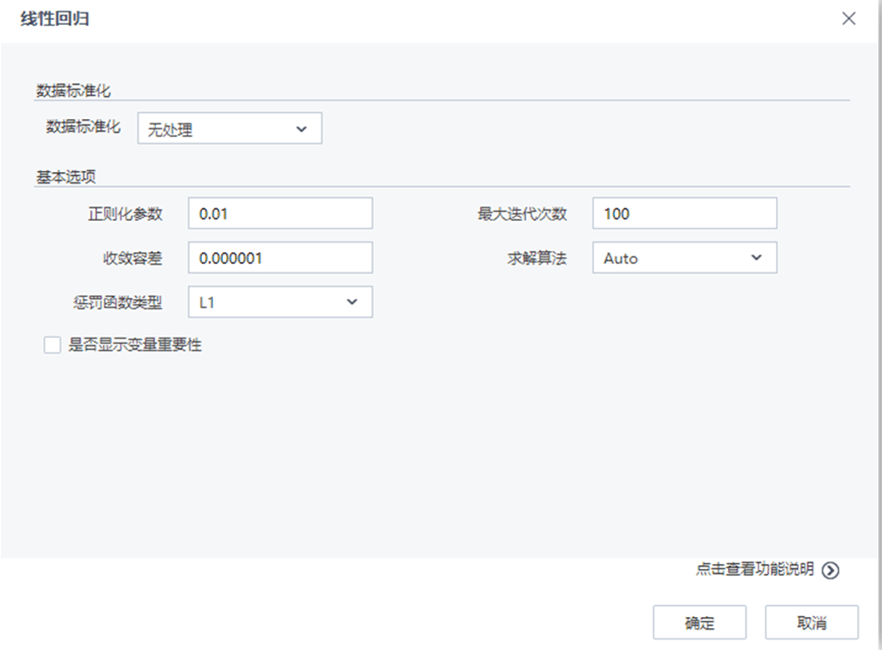
流程運行結果如下：